

Next: 1.1.1 Exact image enhancement
Up: 1 Introduction
Previous: 1 Introduction
1.1 Theory
An optical system's finite resolution is described by its optical transfer
function or OTF
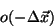 |
(1) |
This represents the signal contribution of a point located an offset
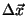 from the point the system is measuring. For a perfect system,
from the point the system is measuring. For a perfect system,
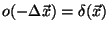 ,
where
,
where
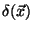 is the Dirac-Delta function. However, for real
systems of finite resolution,
is the Dirac-Delta function. However, for real
systems of finite resolution,
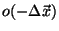 can be measured experimentally
by recording the image
can be measured experimentally
by recording the image 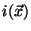 of a very small, point-like source,
acting essentially as a baseline signal. The OTF is then given by
of a very small, point-like source,
acting essentially as a baseline signal. The OTF is then given by
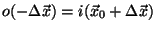 where
where 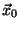 is the (known) position of the point-like source.
is the (known) position of the point-like source.
In addition, as the OTF depends only on the physical nature of the instruments,
it can be analysed to give a theoretical OTF for the system. This is as good
as the OTF obtained experimentally and as shown in Section 2.1.2
has several practical advantages over an experimental OTF.
Equation 1 has been defined in terms of
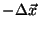 because this means that any measured image
because this means that any measured image 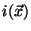 derives from the
original (``true'') image
derives from the
original (``true'') image
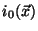 by convolution with the optical
transfer function.
by convolution with the optical
transfer function.
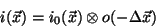 |
(2) |
Now when working in Fourier space, we can use the identity that convolution
is equivalent to multiplication of Fourier transforms to get
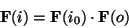 |
(3) |
where the boldface 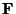 indicates a Fourier transform and the
Fourier transform of the optical transfer function
indicates a Fourier transform and the
Fourier transform of the optical transfer function 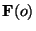 is sometimes
referred to as the point spread function or psf. Quantitatively
sharpening the image
is sometimes
referred to as the point spread function or psf. Quantitatively
sharpening the image 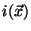 to obtain
to obtain
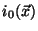 involves
the deconvolution of equation 2, which now
becomes the inversion of equation 3
involves
the deconvolution of equation 2, which now
becomes the inversion of equation 3
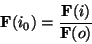 |
(4) |
Unfortunately, real optical systems also suffer from the addition of noise by
the instruments involved in the system. We modify equation 2
to account for the noise 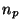 due to a photon
due to a photon 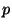 and the optical
instrument noise
and the optical
instrument noise 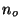 and obtain
and obtain
for the collected noise term
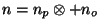 . However,
. However, 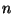 cannot be known and so calculating Equation 5
is no longer possible. Further, considering small
cannot be known and so calculating Equation 5
is no longer possible. Further, considering small 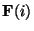 in Equation
4 we see that neglecting
in Equation
4 we see that neglecting  will introduce major disturbances and artifacts in the restored image.
will introduce major disturbances and artifacts in the restored image.
Subsections


Next: 1.1.1 Exact image enhancement
Up: 1 Introduction
Previous: 1 Introduction
Kevin Pulo
2000-08-22
![]() because this means that any measured image
because this means that any measured image ![]() derives from the
original (``true'') image
derives from the
original (``true'') image
![]() by convolution with the optical
transfer function.
by convolution with the optical
transfer function.
![]() due to a photon
due to a photon ![]() and the optical
instrument noise
and the optical
instrument noise ![]() and obtain
and obtain